
1주 2차 논리.
명제 - 논리의 기본 구성요소. 참, 거짓을 명확히 구분할 수 있는 문장이나 수식.
기준에 따라 참, 거짓이 달라지는 경우는 명제가 아님
명제의 진리값 (True value)
-참 : 명제가 타당한 경우. 숫자 1로도 표현한다.
-거짓 : 명제가 타당하지 않은 경우. 숫자 0으로도 표현한다.(이진법)
예시 : 다음 명제의 진리값을 구하여라
(1) 2는 짝수이다 (T)
(2) 소수의 개수는 무한하다 (T)
(3) 3>6 (F)
(4) 대한민국의 수도는 서울이다 (T)
2.논리연산과 논리연산자
1.명제의 종류 :
합성명제
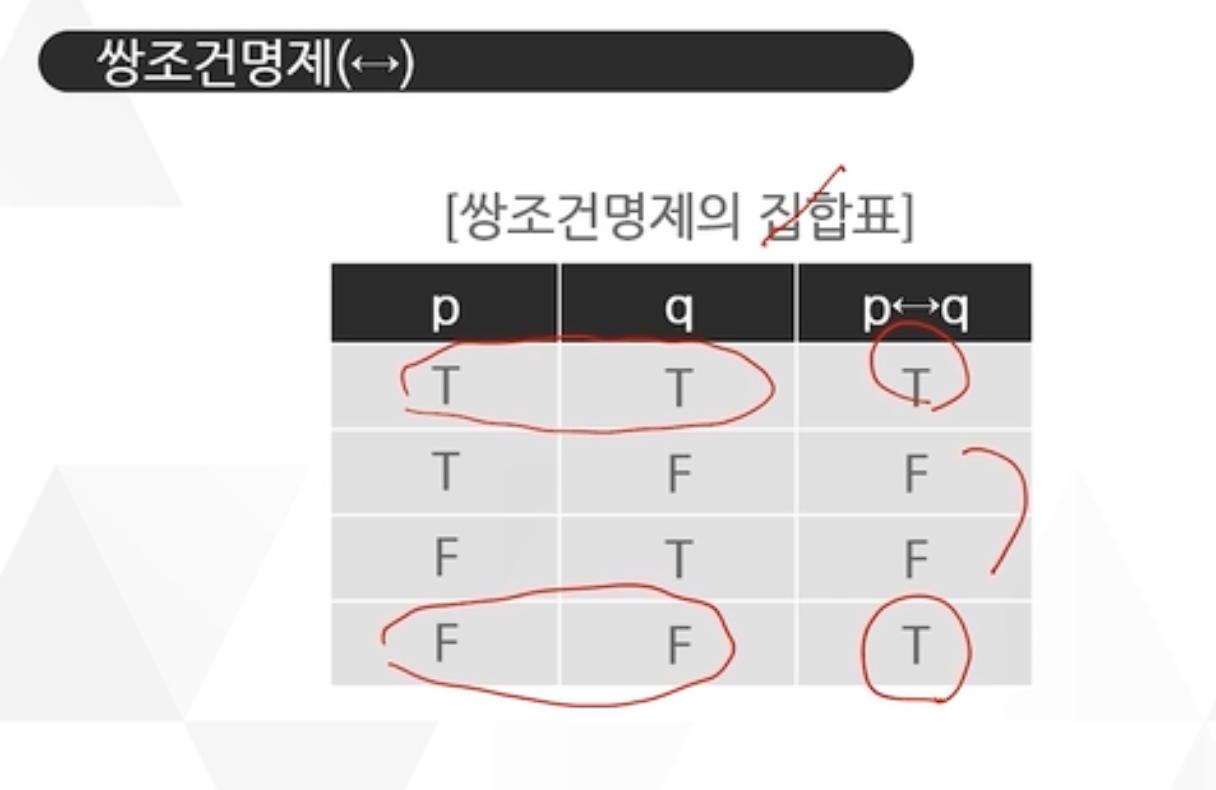
조건명제, 쌍조건명제
항진명제,모순명제
단순명제 -> 더 이상 나눌 수 없는 단위의 명제 (예) '남자는 사람이다.' '5는 3과 같다.'
합성명제 -> 하나 이상의 단순명제가 연산에 의하여 결합되어 만들어진 명제. 복합명제, 겹명제라고도 함. (예) '조지 워싱턴은 미국인이고 도쿄는 영국의 수도이다.'
진리표 -> 단순명제나 합성명제의 모든 가능한 진리값을 나타낸 표. 참여하는 단순명제들이 많을 경우 자연어로 서술하기 어려우므로 진리표를 사용

논리연산자



3.동치






2주차. 술어논리와 추론
술어논리 : 명제논리의 문제점을 해결. 명제를 술어와 주어로 분리하여 술어(주어)의 형태로 표현하기 때문에 주어와 술어 사이에 더욱 세밀한 표현 가능하며 더 다양한 사실을 찾을 수 있음
명제함수 : 변수 값에 의해 함수의 진리값이 결정되는 문장이나 식
한정자 > 전체한정자



2.추론
추론 (Inference) - 참이라고 알려져 있는 사실로부터 논리적인 과정을 거쳐 참인 사실을 이끌어 내는 과정

3.추론규칙 - 어떤 명제로부터 다른 명제나 논리식을 끌어내는 규칙 . 다른 주장들로부터 결론을 도출하는데 사용. 증명의 과정을 연결하는 역할. 가설로부터 논리적으로 결론에 도달하는 과정이 정당하다는 것을 보여줌.


2주차 2차시 (4차시) 증명
공리(Axiom) : 어떤 다른 명제들을 증명하기 위해 전제로 사용되는 가장 기본적인 가정이며 별도의 증명 없이 참(T)으로 이용되는 명제
증명(Proof) : 특정한 공리들을 가정하고 그 가정하에 제안된 명제가 참임을 입증하는 작업
정리(Theorem)
2.수학적 귀납법
3주차 6차시 집합
-카디널리티 : 원소의 갯수



서로소 : 임의의 두 집합에 대해 교집합에 해당하는 원소가 전혀 없는 경우.
멱집합(power set) : 임의의 집합에서 발생할 수 있는 모든 부분집합들을 원소로 갖는 집합

4주차 1차시 행렬






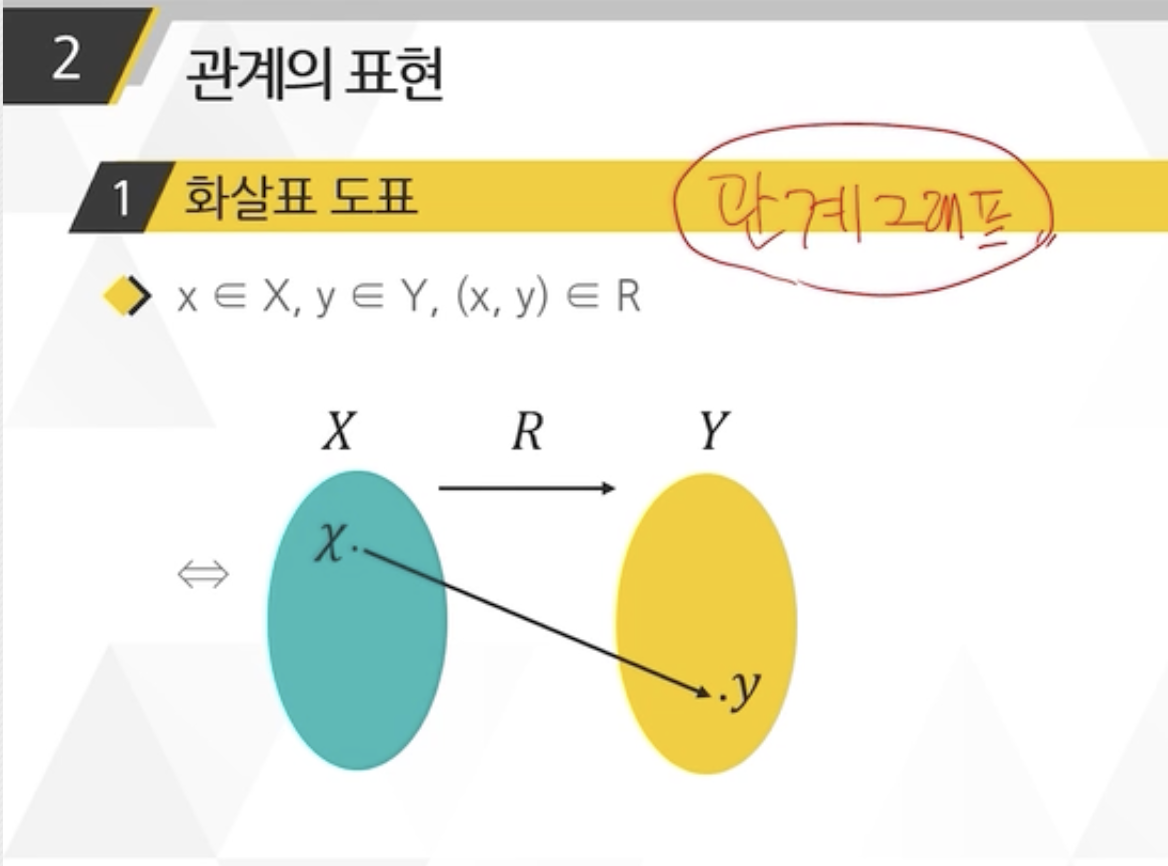
4주차 2차시 관계
관계 : 서로 다른 집합에 있는 원소들 사이의 관련성. 원소들 간의 순서를 고려한 순서쌍의 형태로 표현. 이러한 순서쌍의 집합을 이항관계라 함.














5주차. 1차시 함수

단사함수, 전사함수, 전단사함수

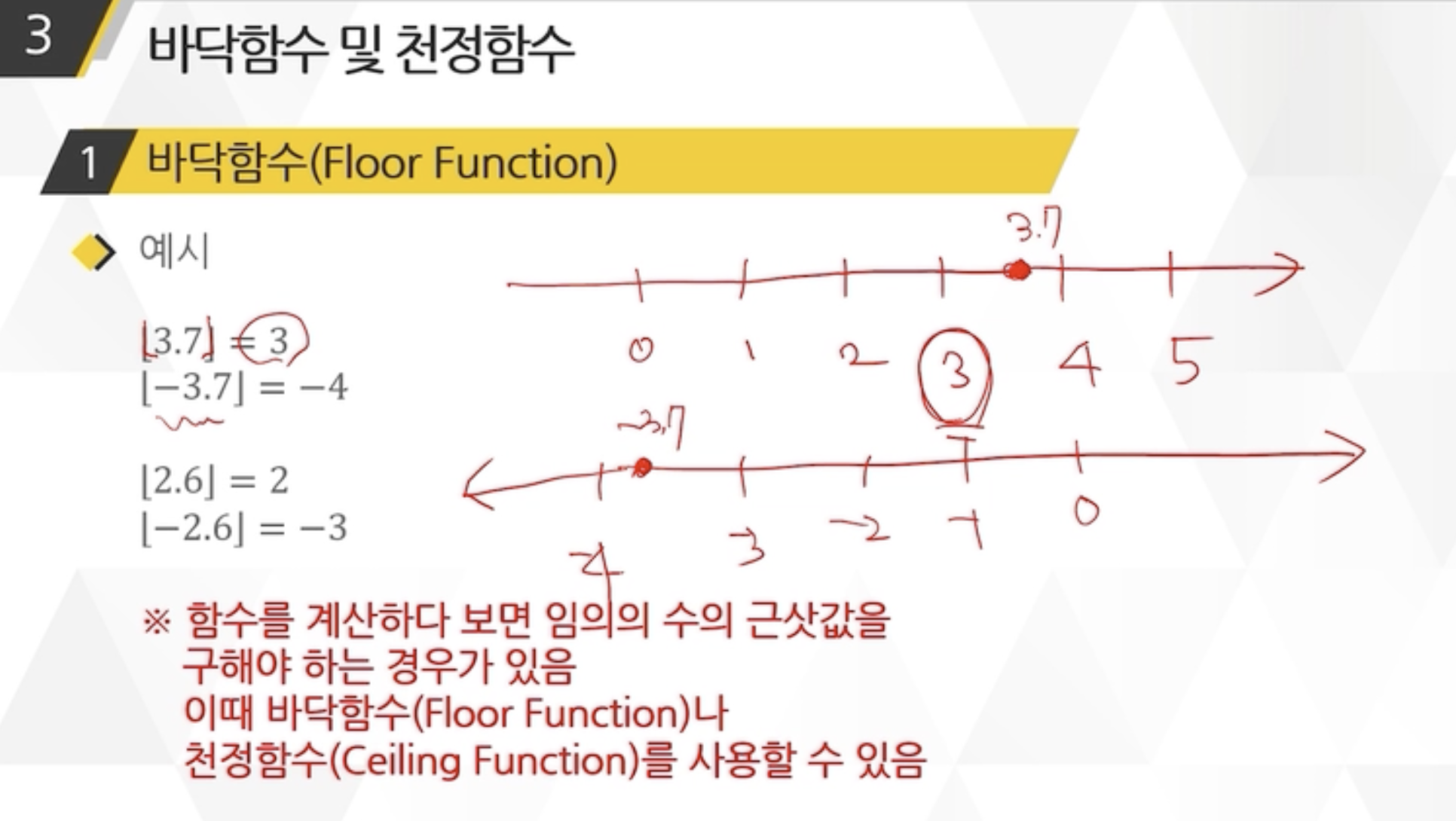
5주차. 2차시 (10차시 ) 함수의 종류

6주차. 1차 부울대수
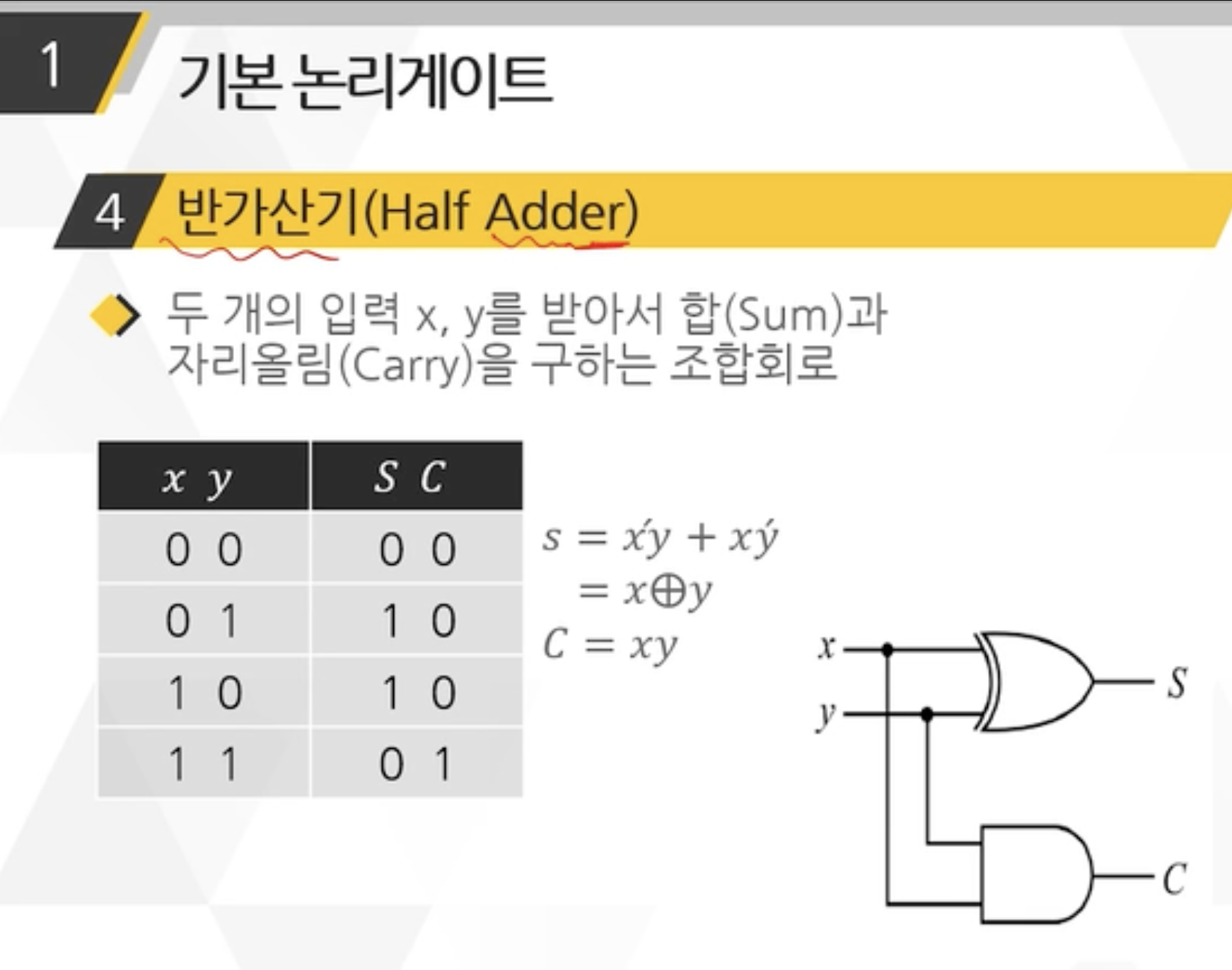
디지털 논리회로 - 디지털 논리회로로는 AND, OR 게이트










6주차. 2차 부울대수의 간소화














'학교 & 학원 이론 수업 > 소프트웨어공학과 수업' 카테고리의 다른 글
| 선형대수학 (0) | 2023.09.04 |
|---|---|
| 공학수학 (0) | 2023.08.31 |
| 데이터통신 (0) | 2023.06.04 |
| 대용량 데이터 처리(k-mooc 교육과정) (0) | 2023.05.21 |
| 선형대수학 (k-mooc 교육과정) (0) | 2023.05.09 |

